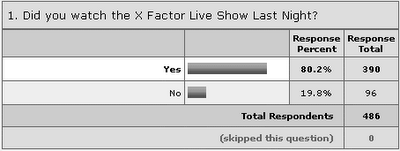
The market for 2nd elimination is already open and The MacDonald Brothers and Dionne are favourites to go. How can anyone sensibly speculate as to who will leave this week without knowing how they will sing on the night? Dionne and The Unconventionals combining to form the bottom two on Saturday night taught us two things: 1) An act relatively popular in the polls can find themselves in the bottom two by performing diabolically on the night (and subsequently exit), and 2) An act unpopular in the polls can perform well and still fail to attract votes, and hence attract the wrath of the judges.
When things appear uncertain, it is often rewarding to remind ourselves of certainties, because they can sometimes be overlooked. At the risk of stating the obvious, here are four of them:
Certainty #1
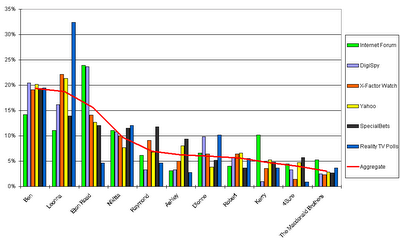
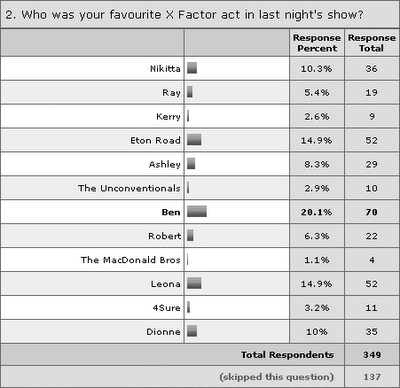
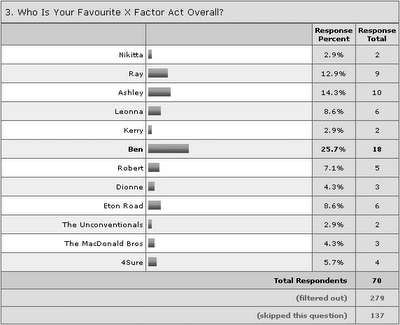
Firstly, we know for certain how the opinion polls have adjusted after last week’s show. To summarise, here is an update of the data posted last week. Only incremental votes post show have been included where possible, and as yet there is no data for realityTVpolls.com (however, I have added a new internet poll, which is rather confusingly called Reality TV Polls.)
And in picture form, the above manifests itself as follows:
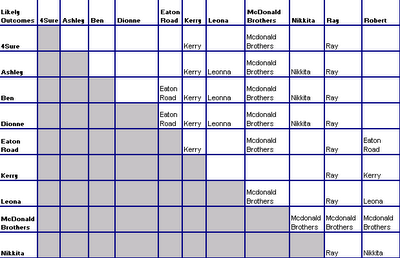
Certainties #2 and 3 We also know for certain that 2 of the remaining 11 contestants will come bottom and face the judges. Combine this with the certainty of knowing which contestants are in which judge’s group, then we can deduce, for each possible bottom pairing, which judge it will be to cast the deciding vote on Saturday night. (note – pairings from the same group will be marked as “open”)
Certainty #4
Our final certainty is how the judges received the contestants last time out. To quantify this, for each remark a judge made to a contestant, I have allocated a score of one to three. A score of one represents adulation, two represents less excited remarks, and three represents comments of a non-complementary nature (of which there were surprisingly few).
Putting together certainties 2,3 & 4 gives some clues as to how the deciding judge will vote assuming that the performances on Saturday night are on a par with those last week. For example, if the final two last week had been Ray and Dionne, who would have gone?
Well, the table above shows us that Louis would have had the deciding vote. Of Ray, Louis said “You’ve got a big smile and a great personality, but you’re gonna have to work hard on your voice.” Of Dionne (the very next act), Louis said “I think you’re the best act so far”. On the basis of these two comments a “Louis” score of 3 for Ray and 1 for Dionne has been allocated. And on that basis, if Ray and Dionne make up the bottom two on Saturday, assuming their performances are on a par with last week, then Ray should leave.
Many pairs are too close to call, and these have been left blank, but filling in the gaps that we can gives the following:
The two burning questions at this stage are – 1) How do we fill in the rest of the table above, and allocate likelihoods to each pairing finishing bottom? And 2) How do we adjust this for variance in the quality of performance in acts from last week?
These are two questions that I am going to spend the next couple of days pondering and attempt to answer before the weekend. A kind of “half-certainty” at this stage is that a contestant that performed well last week but badly this week will have more chance of survival than a repeat offender, and that for some contestants the likelihood of performing badly is greater than that of others. But we are now moving from a deterministic world of certainty into a stochastic one.
Suggestions (polite ones only please!) and discussion would be more than welcome!
Statman
Links
